随机事件

一、基本概念

1. 随机现象与随机试验

随机现象：大量重复观测后，结果表现出某种规律性的现象
统计规律性：随机现象在大量重复观测时所表现出来的量的规律性

随机试验 $E$：为了研究和揭示随机现象的统计规律性，需要对随机现象进行大量重复的观察、测量或者试验

• 可重复性：可以在相同的条件下重复进行
• 可观测性：每次试验的结果都是明确的，可观测的
• 随机性：每次试验要出现哪些结果是不确定的，试验之前无法预知哪一个结果出现

2. 样本空间

Sample Space
样本空间： $\mathrm{\Omega }$ 随机现象一切可能基本结果组成的集合
$\mathrm{\Omega }={\omega }_1,{\omega }_2,\cdots ,{\omega }_n$
样本点： $\omega$ 样本空间的每个基本结果
离散样本空间： 样本点有限、可列
连续样本空间： 样本点不可列

3. 随机事件

随机事件 $ABC$ ：随机现象的某些样本点组成的集合，简称事件，任一事件都是样本空间的子集 $A\subseteq \mathrm{\Omega }$

一次试验中，出现一个样本点 $\omega$

• 如果 $\omega \in A$ 则事件A 发生
• 如果 $\omega \notin A$ 则事件 A 不发生

基本事件：单个样本点 $\omega$ 组成的事件
必然事件：$\mathrm{\Omega }$ 包含样本空间的所有样本点，每次试验必然发生
不可能事件：$\varnothing$ 不包含任何样本点，在每次试验中都不可能发生

4. 随机变量

随机变量： $XYZ$ 定义在样本空间 $\mathrm{\Omega }$ 上的单值实值函数

5. 事件域

Event Space 事件域 $\mathcal{F}$ $\sigma$ 代数
$\mathcal{F}$ 为样本空间 $\mathrm{\Omega }$ 的某些子集所组成的集合类，满足：

1. $\mathrm{\Omega }\in \mathcal{F}$
2. 若 $A\in \mathcal{F}$ 则对立事件 $\bar{A}\in \mathcal{F}$
3. 若 $A_n\in \mathcal{F},n=1,2,\cdots$ 则可列并 $\bigcup _{n=1}^{+\mathrm{\infty }}{A}_n\in \mathcal{F}$

二、事件间的关系

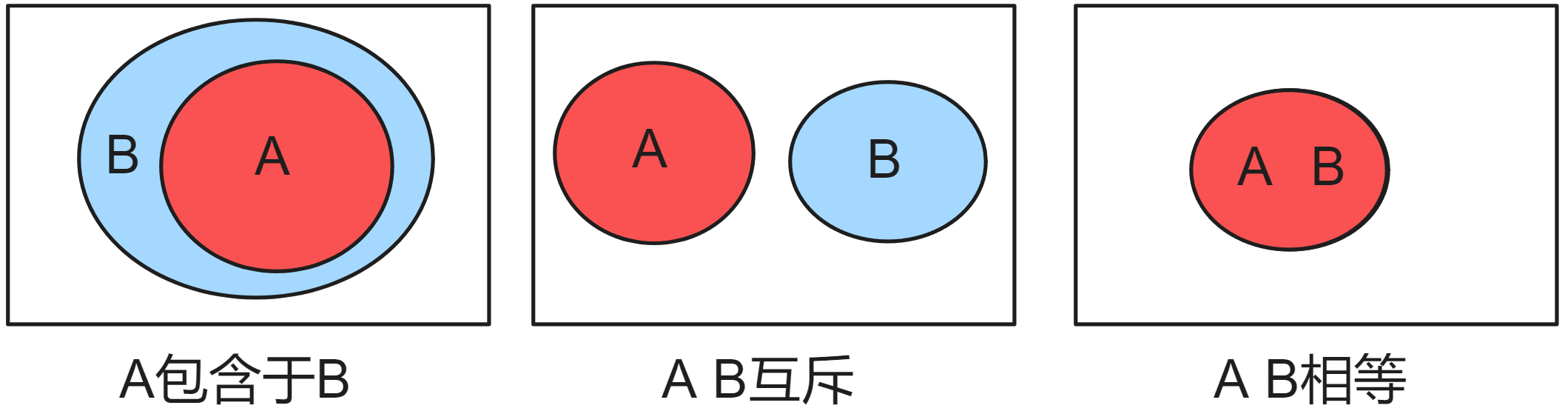
包含： $A\subset B$ 事件 $A$ 的样本点必然属于事件 $B$，当事件 $A$ 发生时事件 $B$ 一定发生

互不相容/互斥：$AB=\varnothing$ 事件 A、B 没有相同的样本点，事件 A、B 不能同时发生

相等： $A=B$ $A\subset B,B\subset A$ 事件 $A$、$B$ 所含样本点完全相同

三、事件运算

逻辑代数

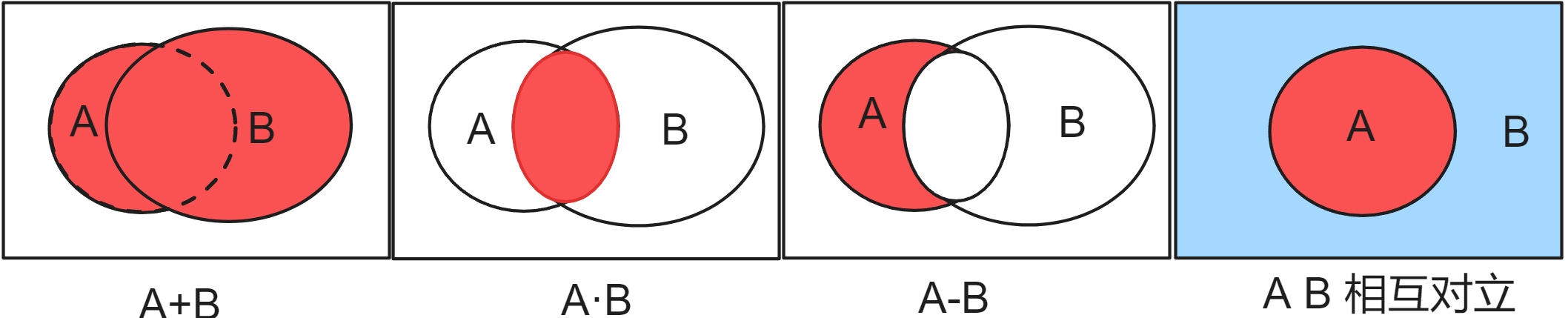
1. 事件的运算

并/和/或 or $A\cup B$ $A+B$
事件 A 和事件 B 中所有的样本点组成的新事件 --> 事件 A 和事件 B 至少有一个发生

• 一般而言 加法公式：$P(A+B)=P(A)+P(B)-P(AB)$
• 事件互斥：$P(A+B)=P(A)+P(B)$

交/积/与 and $A\cap B$ $AB$
事件 A 和事件 B 中公共的样本点组成的新事件 --> 事件 A 和事件 B 同时发生

• 一般而言 条件概率 乘法公式
  $P(AB)=P(B)P(A\mid B)=P(A)P(B\mid A)$
• 如果 A 、 B 相互独立，$P(AB)=P(A)P(B)$

差 $A-B$ $A-B=A-AB=A\complement B$
事件 A 发生而事件 B 不发生
减法公式：$P(A-B)=P(A)-P(AB)$

对立事件 $\bar{A}=\mathrm{\Omega }-A$
$A\cup B=\mathrm{\Omega },A\cap B=\varnothing$, 则称事件 A、B 互逆或对立
互为逆事件，记 $B=\bar{A}$

2. 随机事件的运算性质

交换律：

结合律:

分配律:

对偶律：